El Teorema de Taylor fue enunciado por Brook Taylor en 1712, y permite aproximar una función en un entorno de un punto donde la función sea diferenciable por aproximaciones polinómicas.
Si n ≥ 0 es un entero y f una función que es derivable n veces en el intervalo cerrado [a,x] y n+1 veces en el intervalo abierto (a,x), entonces se cumple que:
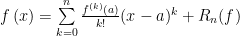Donde 
denota el resto de de aproximar f por el polinomio depende de x y es pequeño si x está próximo al punto a.
y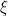 
es un número entre a y x.
En general si la (n+1) derivada de f está acotada por una constante M en el intervalo (a,b) que se menciona en el teorema de Taylor, es decir, si
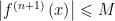para todo x en (a,b)
entonces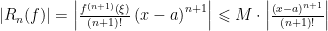
Cuando n crece indefinidamente entonces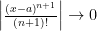
Para algunas funciones se puede probar que el resto se aproxima a cero cuando n tiende a infinito. Dichas funciones pueden ser expresadas como series de Taylor en un entorno reducido alrededor del punto a y se llaman funciones analíticas.
En el caso a=0 tenemos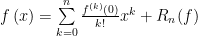
y a esta expresión la llamamos fórmula de Mac Laurin.
Veamos dos ejercicios:
Encontrar la fórmula de Mac Laurin para la función
…
En general observamos que las derivadas de orden par, evaluados en cero se anulan y las impares valen alternadamente 1 y -1.
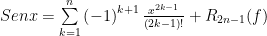
Encuentre un valor aproximado para
utilizando un polinomio de Taylor de grado 3 y estime el error.
Observamos que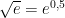
, es decir se nos pide evaluar a la función exponencial en 0.5, el cual es un valor cercano a a = 0, punto en que conocemos a la función exponencial y a sus derivadas.
Así pues encontremos la fórmula de Taylor para f(x) =
en a = 0 y posteriormente evaluaremos en x = 0,5
Como la función exponencial y todas sus derivadas son iguales a 1 evaluadas en 0 tenemos
Evaluada la función en 0,5 tenemos
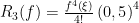
Como![f^4 (x) = e^x \,\,\left| {e^x } \right| < 3\,\,\forall x \in \left[ {0,1} \right]](http://s.wordpress.com/latex.php?latex=f%5E4%20%28x%29%20%3D%20e%5Ex%20%5C%2C%5C%2C%5Cleft%7C%20%7Be%5Ex%20%7D%20%5Cright%7C%20%3C%203%5C%2C%5C%2C%5Cforall%20x%20%5Cin%20%5Cleft%5B%20%7B0%2C1%7D%20%5Cright%5D&bg=ffffff&fg=000000&s=0 "f^4 (x) = e^x \,\,\left| {e^x } \right| < 3\,\,\forall x \in \left[ {0,1} \right]")
entonces 
Si n ≥ 0 es un entero y f una función que es derivable n veces en el intervalo cerrado [a,x] y n+1 veces en el intervalo abierto (a,x), entonces se cumple que:
Donde denota el resto de de aproximar f por el polinomio depende de x y es pequeño si x está próximo al punto a. y es un número entre a y x. En general si la (n+1) derivada de f está acotada por una constante M en el intervalo (a,b) que se menciona en el teorema de Taylor, es decir, si
para todo x en (a,b)entonces
Cuando n crece indefinidamente entonces
Para algunas funciones se puede probar que el resto se aproxima a cero cuando n tiende a infinito. Dichas funciones pueden ser expresadas como series de Taylor en un entorno reducido alrededor del punto a y se llaman funciones analíticas.
En el caso a=0 tenemos
y a esta expresión la llamamos fórmula de Mac Laurin.Veamos dos ejercicios:
Encontrar la fórmula de Mac Laurin para la función
…
En general observamos que las derivadas de orden par, evaluados en cero se anulan y las impares valen alternadamente 1 y -1.
Encuentre un valor aproximado para
utilizando un polinomio de Taylor de grado 3 y estime el error.Observamos que
, es decir se nos pide evaluar a la función exponencial en 0.5, el cual es un valor cercano a a = 0, punto en que conocemos a la función exponencial y a sus derivadas.Así pues encontremos la fórmula de Taylor para f(x) =
en a = 0 y posteriormente evaluaremos en x = 0,5Como la función exponencial y todas sus derivadas son iguales a 1 evaluadas en 0 tenemos
Evaluada la función en 0,5 tenemos
Como
entonces 
No hay comentarios:
Publicar un comentario